ค่าสัมบูรณ์ของจำนวนจริง

นิยามได้ดังนี้: สำหรับจำนวนจริงใดๆ a, ค่าสัมบูรณ์ของ a เขียนแทนด้วย |a| เท่ากับ a ถ้า a ≥ 0 และเท่ากับ−a ถ้า a < 0 (ดูเพิ่มเติม: อสมการ) |a| จะไม่เป็นจำนวนลบ ค่าสัมบูรณ์จะเป็นจำนวนบวกหรือศูนย์  อ่านเพิ่มเติม

การไม่เท่ากัน

การเท่ากันในระบบจำนวนจริงมีสมบัติพื้นฐาน ดังนี้

1. สมบัติการสะท้อนถ้า a เป็นจำนวนจริงใด ๆ แล้ว a = a เช่น 3 = 3

2. สมบัติการสมมาตร  เมื่อ a และ b เป็นจำนวนจริงใด ๆ ถ้า a = b    อ่านเพิ่มเติม

สมบัติของจำนวนจริง

สมบัติการเท่ากันของจำนวนจริง

กำหนด a, b, c เป็นจำนวนจริงใดๆ

1. สมบัติการสะท้อน a = a

2. สมบัติการสมมาตร ถ้า a = b แล้ว b = a

3. สมบัติการถ่ายทอด ถ้า a = b และ b = c แล้ว a = c

4. สมบัติการบวกด้วยจำนวนที่        อ่านเพิ่มเติม

จำนวนจริง

มีหลักเกณฑ์ในการแบ่งจำนวนจริงอยู่หลายเกณฑ์ เช่น จำนวนตรรกยะ หรือ จำนวนอตรรกยะ; จำนวนพีชคณิต (algebraic number) หรือ จำนวนอดิศัย; และ จำนวนบวก จำนวนลบ หรือ ศูนย์

จำนวนจริงแทนปริมาณที่ต่อเนื่องกัน โดยทฤษฎีอาจแทนได้ด้วยทศนิยมไม่   อ่านเพิ่มเติม

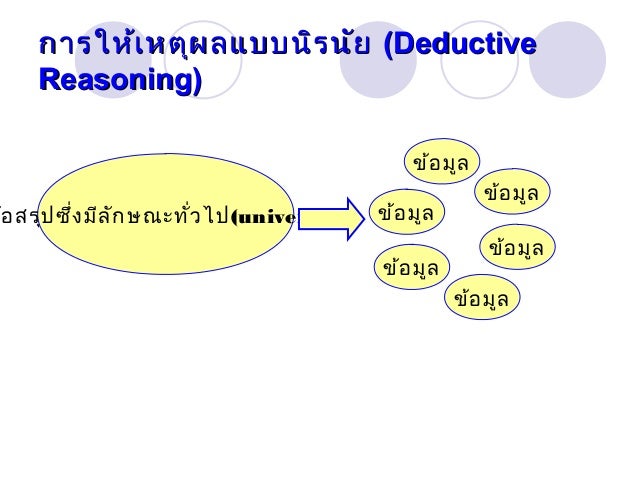
การให้เหตุผลแบบนิรนัย

การให้เหตุผลแบบนิรนัย (Deductive Reasoning ) เป็นการนำสิ่งที่ยอมรับว่าเป็นจริงมาประกอบเพื่อนำไปสู่ข้อสรุปจากสิ่งที่ยอมรับแล้ว

         - การสรุปที่สมเหตุสมผล (Valid) คือ ข้ออ้างหรือเหตุที่เป็นจริงเป็นผลให้   อ่านเพิ่มเติม

การให้เหตุผลแบบอุปนัย

1การให้เหตุผลแบบอุปนัย (Inductive Reasoning) เป็นการสรุปผลในการค้นหาความจริงจากการสังเกต  หรือการทดลองหลายครั้งจากกรณีย่อยๆ แล้วนำมาสรุปเป็นความรู้แบบทั่วไป ซึ่งข้อสรุปที่ไม่จำเป็นต้อง   อ่านเพิ่มเติม

ยูเนียน อินเตอร์เซกชันและคอมพลีเมนต์ของเซต

1.	ยูเนียน (Union)	ยูเนียนของเซต A และ B คือเซตที่ประกอบด้วยสมาชิกของเซต A หรือ B เขียนแทนด้วย A  B
2.	อินเตอร์เซคชัน (Intersection)	อินเตอร์เซคชันของเซต A และ B คือเซตที่ประกอบด้วยสมาชิกของเซต A และ B เขียนแทนด้วย A  B
3.	คอมพลีเมนต์ (Complement)	คอมพลีเมนต์ของเซต A คือเซตที่ประกอบด้วย   อ่านเพิ่มเติม